Illustration by Annie Rosen
Dr. Neil Ashby is a professor at the University of Colorado, Boulder. His research emphasizes the practical applications of theoretical general relativity.
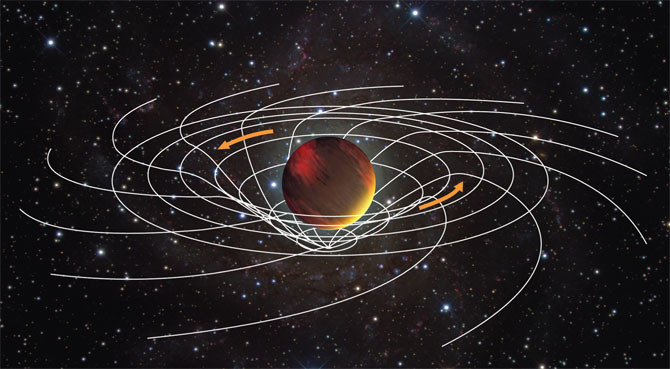
The idea behind frame dragging is that a spinning body—or, more specifically, any moving body—tends to have a gravitational effect that propagates through empty space (aka the vacuum) and drags things along with it. This is peculiar because if you put a gyroscope near the axis of a spinning body, it’ll tend to be pulled around in the direction of the spin. But if you place it outside the equator of the same body, then the moving mass drags the gyroscope around the other way.
Let’s use our spinning Earth as an example. The effect of its spinning on its neighborhood is very tiny because it’s not going very fast and it’s not a huge astronomical body. Nevertheless, if a satellite is orbiting Earth, then it will become a gyroscope. The axis of the gyroscope is perpendicular to the orbital plane of the object that’s being dragged around by Earth. If you look at the orientation of the two objects by using an astronomical reference point—distant stars that are very nearly fixed, for example—you can look at the orbit in relation to those distant stars to see that the orientation is turning. The equatorial plane of Earth extends out into space, and at a certain point the orbit of the satellite will go from south to north, through this plane. This is called the nodal point. As the orbit turns, that point will move. Imagine this equatorial plane and the orbital plane of the satellite turning, and as they do, the point of intersection turns. The line intersecting those two planes, which turns a tiny bit, is called the line of nodes.
This concept can also be applied to a binary neutron star system: two very dense, rapidly rotating objects in close proximity. The gravitational field of one spinning object will cause the axis of the other object to turn. Whenever you have a massive spinning object—and the more massive it is and the more spinning, the bigger the effect—the orbits of satellites around it will reverse.
Because of the frame-dragging effect, someone watching a binary neutron star system from afar would observe that the satellites around that system progress in a different timeline. That is, for things lower in the gravitational field, the clock tends to run slower. These kinds of effects are commonplace on Earth when dealing with the Global Positioning System. Because that system is so precise, one must worry about the clocks in the satellites running faster than those on Earth. They have to be compensated for.
Now imagine that massive binary system again. The sheer massiveness of the two neutron stars will affect time much more drastically. For anyone used to the comparatively mild Earth time shift, it will be a mess. All measurements of time will depend on how close the clock is to one of the other stars, and so on. Another way we can observe this effect on Earth is by watching the orbit of satellites. Picture two satellites in line with Earth, with one object behind the other. In this scenario, light from the object behind is going to pass near the surface of the other and slow down. That is, the actual speed of the light will decrease.
The experiments executed to measure the frame-dragging effect are involved, to say the least. The LAGEOS satellites, for instance, are a series of spacecraft full of lead and covered with reflectors that laser beams are bounced off of. By measuring the time it takes for the beam to bounce back, it’s possible to derive the satellite’s orbit using millions of such measurements. Of course, there are other effects that cause the line of nodes to turn, and that’s been a major stumbling block in the attempt to detect frame dragging. Earth’s flattening (at the poles), or axial tilt, for instance, causes the line of nodes to turn. We must wait for better models of Earth’s gravitational field—models that account for these stumbling blocks—before we can really see general relativistic frame dragging.